先学期の大学の講義で「ベキ則にしたがう現象の例を挙げ,実際に成り立つことを確認せよ」という趣旨のレポート課題が出されました.そこで,自然言語では一般に成り立つことが知られている Zipf の法則が,TeX 言語のコードにおいても成り立つかどうかを調べました.本稿では,この実験の結果について簡単にまとめてみようと思います.
ベキ則と Zipf の法則
ベキ則は極めて広範な対象において観察される経験則で,簡単に言えば様々なデータを集めた際にその分布が \[ p(x) = Cx^{-\alpha} \] のような形で表される現象のことを言います.
ベキ則の一例として,言語学や自然言語処理の分野では「出現頻度が $k$ 番目の要素が全体に占める割合は $1/k$ に比例する」という Zipf の法則が有名です.この法則は実際に多くの自然言語で書かれたテキストにおいて成り立っています.
解析用 Python スクリプト
TeX 言語において Zipf の法則が成り立っているかどうかを調べるため,TeX コード中に現れる制御綴を収集し,各制御綴の出現回数を数え上げます.TeX 言語を厳密に字句解析するのはかなり難しいですが,以下のような制約を入れれば簡単に解析することができます.
- コードの途中で,カテゴリーコードは変更されないものとする
\csname等により動的に生成される制御綴は考慮しない
実際,一般的な TeX (on LaTeX) コードにおいて明示的に使用されている制御綴はこの制約下でも十分に収集することができます.このとき「制御綴」はカテゴリーコード0の文字 \ に後続する
- 連続したカテゴリーコード11の文字
a-z,A-Z,@の列(コントロール・ワード) - カテゴリーコード11以外の1文字(コントロール・シンボル)
です.これは正規表現で簡単にマッチすることができますね.
あとはマッチした各制御綴の出現回数を数え上げるだけで今回の目的を達することができます.
以下はファイルパスを指定して実行すると,そのファイルに含まれる制御綴の出現順位と出現回数の関係をプロットしたグラフを出力する簡単な Python スクリプトです.動作確認は Python 3.6.2 で行いました.
latex.ltx の解析
上記の Python スクリプトを用いて,LaTeX2e のカーネル(latex.ltx)中に登場する制御綴の出現順位と出現頻度の関係を両対数グラフにプロットしました.以下に示すのはその結果です.
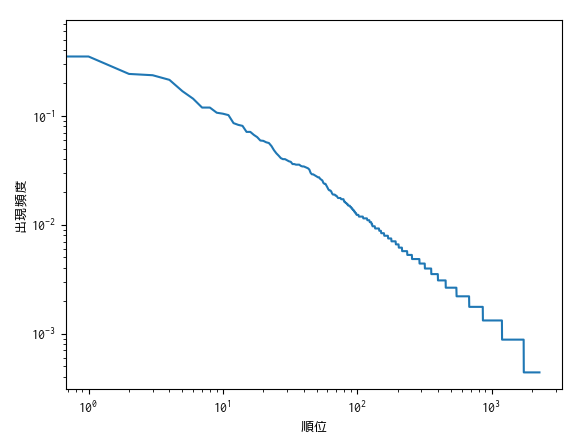
これを見ると概ね傾きが $-1$ の直線上に乗っており,Zipf の法則が成り立っていると言えそうです.
蛇足ですが,latex.ltx に登場する制御綴の頻度を調べたので(特に TeX 言語者の場合)その上位の顔ぶれが気になることでしょう.ということで,出現頻度ベスト10を表にしてみました.
| 順位 | 制御綴 | 出現回数 |
|---|---|---|
| 1 | \def | 1221 |
| 2 | \fi | 798 |
| 3 | \expandafter | 552 |
| 4 | \let | 537 |
| 5 | \else | 487 |
| 6 | \relax | 383 |
| 7 | \z@ | 327 |
| 8 | \endcsname | 271 |
| 9 | \csname | 271 |
| 10 | \global | 243 |
堂々の第一位はマクロ定義を行う \def でした.TeX 言語は(究極的には)あらゆるモノをマクロ定義で表現する言語なので,この結果は当然と言えると思います.\if よりも \fi が多いのは,TeX 言語を書かない人にとっては非直感的かもしれませんが,TeX 言語において条件分岐に関わる命令は \if, \ifx, \ifnum 等々多数ある一方で,そのすべてが \fi で閉じられるのでこのような結果になります.皆さんの大好きな \expandafter は第3位にランクインしていますね.なお,完全な順位表を以下の URL で公開しています.
(2019-04-04 編集:リンク先を Gist に変更)
その他の解析
latex.ltx についてのみ解析を行って「TeX 言語でも Zipf の法則が成り立っている」と主張するのは少々強引なので,他のファイルについても同様の解析をしてみました.
plain.tex
Knuth の作成したマクロ体系(フォーマット)である plain.tex も LaTeX と同様に @ をカテゴリーコード11として扱っているので,同じスクリプトを用いて解析することができます.結果は以下の通りで,latex.ltx ほど綺麗ではありませんが,それでもなんとか傾き $-1$ の直線上に乗っていると言えそうです.
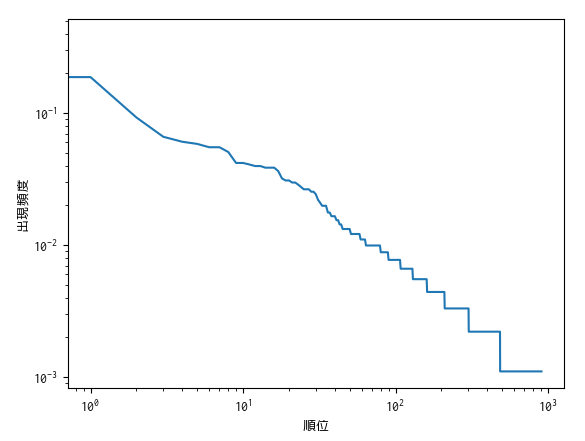
tcolorbox.sty
また,一般の LaTeX パッケージを解析する例として,近年 LaTeX 文書において「装飾用の枠」を描画するのに定評のある tcolorbox パッケージについても同様のグラフを出力してみました.
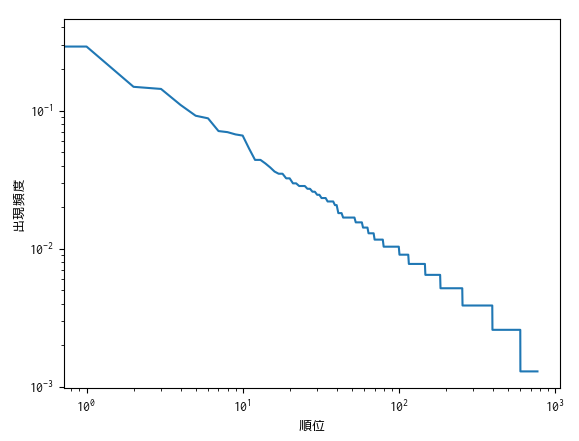
tcolorbox ではここまでに示したいずれのグラフよりも綺麗に Zipf の法則が成り立っているようです.
なお,他のさまざまな LaTeX パッケージについても,先述のスクリプトを用いて同様に解析できるはずです.特に,TeX Live 利用者の場合は
$ python ccs.py `kpsewhich <package>.sty`
などと叩くのが簡単でしょう.
ただし,一般に Zipf の法則が成り立っていることを確認するには,ある程度コード量があるものを対象とする必要があります.また,私の簡易スクリプトはファイル読み込み(\input, \RequirePackage など)に対応していないため,単一ファイルで構成されているパッケージでない限りはそのまま流用することはできないので注意してください.
考察
人工言語においても Zipf の法則が発現するという結果は特に新しいものではなく,古いですが例えば以下の論文がそのようなことを述べています.
これによると,コマンド言語(人工言語)が,特にユーザによってカスタマイズされると,Zipf の法則にしたがうような頻度分布を示す傾向があるとされています.TeX 言語におけるマクロの機能はまさにユーザによるコマンド(制御綴)のカスタマイズにあたるものなので,今回の結果はその具体例と言えるでしょう.
TeX 言語(TeX on LaTeX)はこのように Zipf の法則が成り立つ好例であるばかりでなく,正規表現を用いて制御綴の簡易的な識別を容易に行うことができるため,今回の調査を行うにあたって非常に扱いやすい言語でした.シェルスクリプトや C 言語などについて同様の解析をしようと思っても(問題の定式化方法にもよりますが)もう少し手間がかかるだろうと思います.
こうした調査の応用としては,これらの結果を新しいマクロ体系(フォーマット)や LaTeX のクラス・パッケージなどを設計する際の参考にすることが考えられます.
ユーザによる最適化と Zipf の法則の発現の関係についてはより深く解析していく必要がありますが,もしこれらの間に何らかの因果関係があるとすれば,設計したプロダクトの一般的な使用例において Zipf の法則が成り立つかどうかが,設計の良し悪しを判定する1つのバロメータになり得ます.また,調査の副産物である頻度表を用いることで,高頻度で使用されるユーザ用命令の「長さ」を最適化することも有効でしょう.